The Walk Forward/Out-Of-Sample Metric Surface Explorer

What Is The Surface Gradient?

Before we can describe what the Walk Forward/Out-Of-Sample Metric Surface Explorer does we have to define what a surface and gradient are and why they are important. Each optimization run consists of the strategy input parameters that are varied over a range of values and the associated performance metrics for each of the input parameter cases. One common performance metric is total net profits (tnp). If we had only two strategy input parameters then we could construct a three dimensional (3D) plot where the x and y axis were the two input parameters and the z vertical axis was the associated performance metric for each of the x and y points.
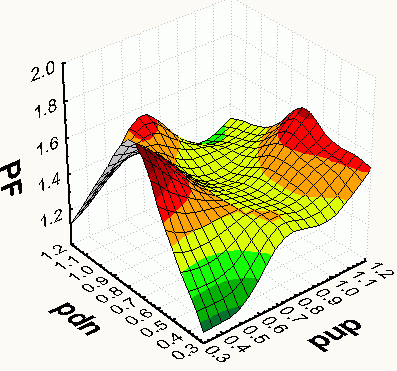
An example of such a 3D plot is to the left where we have chosen the Profit Factor (PF) as the performance metric. Such a plot is called a 3D surface plot. Notice on this Profit Factor surface plot that there are sharp peaks and flat plateaus. The sharp peaks are due to curve fitting the signal and the spurious price movements (noise) with a selected set of input parameters that just by chance match the signal and noise and produce good results. The flat plateaus represent a range of input parameters that produce good results. Because there is a large range of parameters in the surface's flat plateaus that produce good results there is less chance that this range of parameters are curve fitting the noise. The flat plateaus represent robust input parameters that have a greater chance of producing good out-of-sample results.

With only two inputs it's easy, although a bit time consuming, to graph up the 3D surface chart and find the flat plateaus. With three or more inputs we need a 4D or nD graph which we cannot display. In addition if we wanted to examine many optimization test section 3D surface graphs to find the robust input parameters to test on out-of-sample data the analysis time would be enormous. Is there an easy way to mathematically find the flat plateaus without visual inspection so that we can computerize this procedure? The answer is yes and it is called by the mathematical term gradient. We are all familiar with the meaning of the slope of a 2D plot. When the 2D plot moves horizontally the slope is zero and when the line on the 2D plot starts to move up the slope increases in value. For higher dimensional plots the equivalent of slope is called the gradient. The gradient is a measure of the steepness or flatness of an n dimensional surface. The gradient exactly equals the slope when there is only a 2 dimensional plot. We now have a measure, called the gradient, of the flatness of an n dimensional surface so we can let the computer find the minimum absolute value of the gradient or best flatness of our surface. Because this is now done by computer we are no longer restricted to just the total net profit surface. We can have the computer examine all performance variable surfaces (like the profit factor above or Drawdown,etc) , find their minimum gradients and report back which performance variable surface gives us the best out-of-sample results! The Walk Forward Surface Explorer is able to examine up to seven dimensional surfaces. A 7D surface would be 6 input axis vs a selected performance variable.

The Walk Forward Surface Explorer(WFSE)

The Walk Forward Surface Explorer(WFSE) reads each of the files generated by the PWFO and calculates the minimum gradient for each of the PWFO performance variable surfaces. A example of a performance variable surface would be a plot of the total net profits vs the inputs, the Profit Factor vs the inputs, etc. The WFSE then finds the out-of-sample profits associated with each surface's minimum gradient for each file. The WFSE sums each file's out-of-sample results for each of the surface's minimum gradients and finds the statistically best out-of-sample returns for each performance variable surface. Here you can statistically prove whether the total net profits are the best surface to examine or whether there are more robust performance surfaces that give better out-of-sample results. The WFSE is a stand alone exe program that is super fast and automatically displays it's statistical summary and results in Excel.

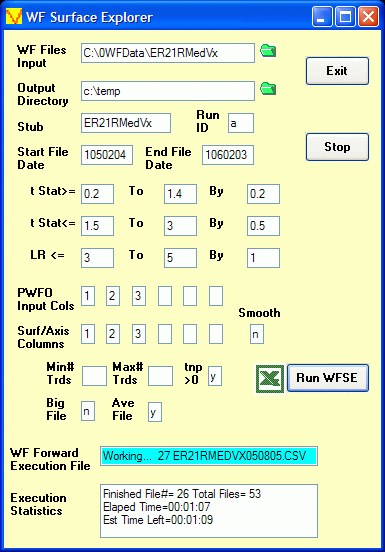Click here to see the WFSE Input Form and a description of the inputs

Data Mining and Curve Fitting. Data mining or curve fitting a price series will always produce the best performance results. If you look hard enough using optimization you will always find patterns in the price data. But they are not real. Why use the PWFO walk forward technique? Why not just perform the TradeStation optimization on the whole price series and choose the input parameters that give the best total net profits or profit factor? Whenever you run a optimization (combinatorial search} over many different combinations of input parameters on noisy data on a fixed number of prices, no matter how many, the best performance parameters found are guaranteed be due to "curve fitting" the noise and signal. When we run, say, 5000 different input parameter combinations , the best performance parameters will be from those system input variables that are able to produce profits from the price pattern and the random spurious price movements. While the price patterns, if there, will repeat, the same spurious price movements will not. If the spurious movements that were captured by a certain set of input parameters were a large part of the total net profits, then choosing these input parameters will produce losses when traded on future data. These losses occur because the spurious movements will not be repeated in the same way. This is why system combinatorial searches with no out-of-sample testing cause loses when traded in real time from something that looked great in the test section.

In order to gain confidence that our system input parameter selection procedure on test data will produce profits "on average" in the future we must perform the walk forward out-of-sample analysis many times. Why not just do the analysis once? Well just as in poker, where there is considerable vagaries in hand to hand luck, walk forward out-of-sample analysis give considerable vagaries in week to week out-of-sample profit "luck". That is, by pure chance we may have chosen some input parameters that did well in the test section data and the out-of-sample section data. In order to minimize this type of "luck", statistically, we must repeat the walk forward out-of-sample (oos) analysis over many test/oos sections and take the average of our weekly results over all out-of-sample sections. This average gives us an expected weekly return and a standard deviation of weekly returns which allows us to statistically estimate the expected equity and it's range for N weeks in the future.

The Walk Forward Surface Explorer Output

Below are snippets of two outputs from two WFSE runs sorted by the average out-of-sample profit per trade (aanp). These examples shows the partial output files from two WFSE runs on the PWFO files generated by the Polynomial Velocity System that was run on E-Mini 1 minute bars for the 26 weeks of 6/11/04 to 12/03/04. The Polynomial Velocity system has four inputs. pw (The polynomial power), n (the lookback period) vup (the upper velocity breakout level), and -vdn (the lower velocity breakout level).

---

The output below is a 5 dimensional (5D) surface run. The 5D surface is constructed from the four inputs vs the performance variable. In 5D space (which cannot be plotted), for each set of input values of pw, n, vup and vdn there exists a value for the performance variable which would be the surface. If the performance variable was Total Net Profits (tnp) then each input value of pw, n, vup and vdn would have it's associated tnp for this system. For the 5D run below the best Surface Performance Variable with the minimum gradient that the WFSE program found was "mru" . "mru" is the performance statistic = Median of {Maximum Trade Profit (run-up) minus Trade Profit for each trade}. t04txx|3:19 means t stat>= 0.04, t stat<=any, lr<=3, and minimum number of trades in test section >=19. The minimum gradient is found for all rows of the PWFO file that are left after the t04txx|3:19 filter is applied.

---

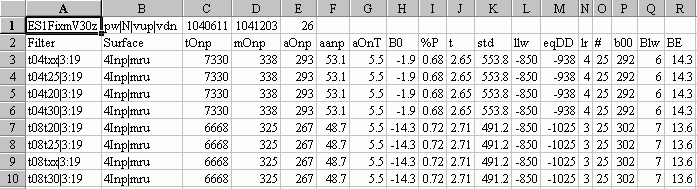
The output below is a 4D surface run. Here a slightly different approach is taken. There are four input values for the Polynomial Velocity System. First we separate the data for each polynomial power pw. Then for that set of data with the same pw we create a 4D plot consisting of N, vup, vdn, and the performance variable. We then calculate the minimum gradient for that 4D surface. We repeat this for each pw input value. This will produce pw different minimum gradients. We then choose the minimum of the pw different minimum gradients. The results are shown below. As you can see for this system the 4D surface produced better results than the 5D surface method.

---

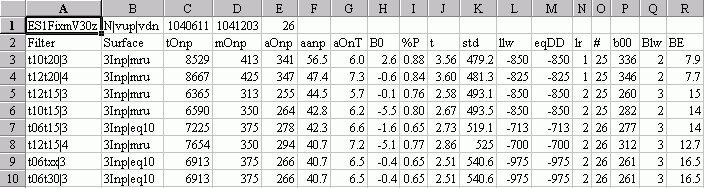
The WFSE Columns are defined as follows

• Row 1
  • The PWFO Stub
  • The Input Parameters Used as Axis For The Surface
  • The PWFO File Start Date
  • The PWFO File End Date
  • The Number of weeks
• Filter = The particular gradient filter. For row 3 of the 5D run, t04txx|3:19 means t stat>= 0.04, t stat<=any, lr<=3, and minimum number of trades in test section >=19.. Click here to see the WFSE Input Form and a description of the inputs
• Surface = The number of input axis and the surface performance variable.
• Each filter and Var produce the following statistics.
• tOnp = Total out-of-sample(oos) net profit for these N weeks.
• mOsp = median out-of-sample net profit for the N weeks
• aOsp = Average out-of-sample net profit for the N weeks
• aanp = Average out-of-sample profit per trade
• aOnT = Average number of out-of-sample trades per week
• B0 = The N week trend of the out-of-sample weekly profits
• %P = The percentage of out-of-sample weeks that were profitable
• t = The student t statistic for the N weekly out-of-sample profits. The higher the t statistic the higher the probability that this result was not due to pure chance
• std = The standard deviation of the N weekly out-of-sample profits
• llw = The largest losing out-of-sample week
• eqDD = The out-of-sample equity drawdown
• lr = The largest number of losing out-of-sample weeks in a row
• # = The number of weeks this filter produced a case. Note for some weeks there can be no cases that satisfy a given filter's criteria.
• b00 = The straight line trend of the out-of-sample equity curve in $/week.
• Blw = The maximum number of weeks the oos equity curve failed to make a new high.
• BE = Break even weeks. Assuming the average and standard deviation are from a normal distribution, this is the number of weeks you would have to trade to have a 98% probability that your out-of-sample equity is above zero.
• Notice: Past performance is no guarantee of future results

The Walk Forward Surface Explorer comes with a detailed manual explaining:

• How to setup and install the Walk Forward Surface Explorer. The Walk Forward Surface Explorer is a stand alone exe file that can be executed directly from your desktop icon or from the Windows Start Program menu.
• How to use the WFSE with your PWFO files.
• An explanation of each of the performance statistics columns.
• Walk Forward Optimization tutorial.

The WFSE Input Finder Excel Add-In and WFSE Strategy Input finder EXE.

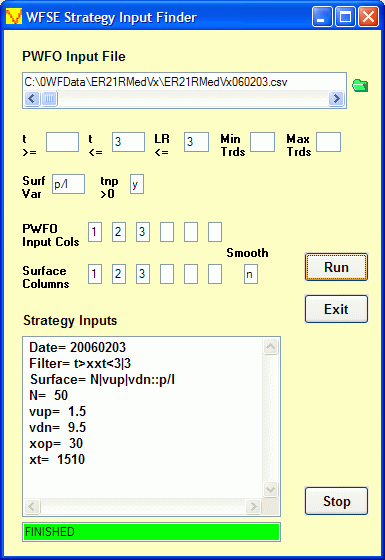
Supplied with the WFSE is an Excel Add-In Filter and a separate WFSE Input Finder EXE. For the Excel Add-In, as shown below, you just click on a special Add-In icon on the Excel Toolbar and a popup window displays. Fill in the WFSE parameters and click on the Run button and the Excel Add-In macro will will display the PWFO Excel file row that satisfies the typed in criteria. The Excel Add-In macro will filter any number of PWFO files loaded in Excel. For the WFSE Input finder, as shown below, fill in the WFSE parameters click on Run and the Strategy Inputs are displayed as shown below.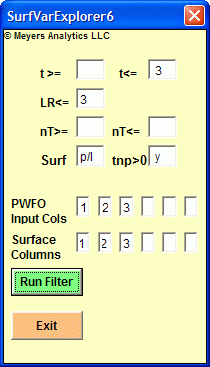

   

The The Walk Forward Surface Explorer package consisting of Manual, EXE file, Excel Add-In and WFSE Strategy Input Finder EXE is being offered, for $325 plus shipping. Please note that the WFSE will only read files generated by the PWFO product. The WFSE has a "Key Licence" that allows it to be installed on only three computers.
How To Order
To order online click Order Online. If you would like to talk to me about the product, please call me at (305) 549-5843 M-F 12pm to 5pm CST. All E-mail queries can be sent to support@meyersanalytics.com.

Thank you for your Interest....Dennis Meyers

---